Some Fractal Aspects in Biopharmaceutics and Pharmacokinetics Review
Israa Al-Ani 1, Fatima Tawfiq 1, Zainab Zakarya 2, Wael Abu Dayyih 2*
1 Faculty of Pharmacy, Al-Ahliyya Amman University, Amman, Jordan.
2 Faculty of Pharmacy and Medical Sciences, University of Petra, Amman, Jordan.
ABSTRACT
The classical kinetic models dealt with homogeneous systems and homogeneous processes or what is called well-stirred systems. However, the thorough study of nature and the human body revealed the fractal nature of it, and the linearity between the input and output is no longer valid. System of fractal and disordered nature demanded satisfactory under dimensional constrains. In this review, some of those efforts are discussed. Fractal aspects in drug absorption from the gastrointestinal tract after oral dosage form was described by many models, here we emphasized only those which related to the derivation of time-dependent absorption rate coefficient. Also, for drug distribution, the description of heterogeneity of process related to blood vessel structure was proposed. For drug elimination, the emphasis was put on the derivation of a new form of Michaelis –Menten equation based on time dependency and fractal rules to describe drug metabolism as a key elimination process.
Key words: Fractal kinetics, heterogeneous processes, modified Michaelis - Menten equation.
INTRODUCTION
Fractals in mathematics are infinitely complicated abstract objects used to describe and simulate naturally occurring objects. Fractals commonly exhibit similar patterns at increasingly small scales also known as expanding symmetry [1]. If this replication is the same at every scale, it is called a self-similar pattern [2]. Fractals can also be nearly the same at different levels.
The work of Mandlbroth in fractals had a huge contribution to the aspects of "fractals" in mathematics which opened the door to many observations [3].
One way that fractals are different from finite geometric figures is how they scale. Doubling dimension of some geometrical shapes results in increasing its area increased more than double like the polygon [4]. And thus, a power law can be extracted. However, if a fractal's one-dimensional lengths are all doubled, the spatial content of the fractal scales would be by a power that is not necessarily an integer. This power is called the fractal dimension of the fractal object, and it usually exceeds the fractal's topological dimension [5,6].
Biopharmaceutics and pharmacokinetics are the bridge between drugs in dosage form and drug in the receptor sites. Biopharmaceutics examines the interrelationship of the physical/chemical properties of the drug, the dosage form (drug product) in which the drug is given, and the route of administration on the rate and extent of systemic drug absorption [7]. Pharmacokinetics (PK) is the study of the time course of the absorption, distribution, metabolism, and excretion (ADME) of a drug, compound, or new chemical entity after its administration to the body [8].
Dealing with biopharmaceutical PK processes needs an understanding of the human body as part of nature. Since fractal structures and processes are now observed in the living things, the study of the human body on this base becomes necessary. For example, lungs, vascular system, neural networks, the convoluted surface of the brain showed fractal structures [9]. Also, with the surface of materials like drug particles, fractal geometry is observed [10]. These observations enabled scientists to put a more realistic explanation of biological processes and reactions.
The fractal aspects in nature and measuring fractal dimensions depends on two things; first, the self-similarity and second, is the scaling power law.
Self-similarity simply means when the object is examined, smaller parts are similar to the larger ones. So, the dimension of this object depends on the number of decreasing self-similar objects. This dimension is called "capacity dimension" [11].
The power scaling is the quantification of a process in which the fractal objects go in. This means the observation is calculated as a result of the power relation of the income and outcome [12].
So, dimensions of fractal objects are described sometimes as non-integer unlike the classical way of 1,2 and 3- dimensions calculations [13].
The degree of irregularity of a fractal object is quantified with a “fractal dimension” (df). Several equations were proposed to calculate this dimension using self-similarity rules or power laws [10].
Fractal aspects of oral drug absorption
There are three different definitions of drug absorption. Traditionally, absorption occurs when the drug reaches the systemic circulation, or sometimes when it reaches the portal vein bloodstream. In recent years, a new definition is presented, in which drug is assumed to be absorbed when it leaves the lumen and crosses the apical membrane of the enterocytes lining the intestine. It is important to distinguish among these definitions when the kinetics study is performed [6].
The complex interrelationships between drug properties and the gastrointestinal characteristics have always made prediction and quantification of drug absorption a difficult task.
Drug absorption depends on multiple factors, from the physicochemical properties of the drug such as solubility and permeability to the physiological factors and variables that contribute to this process [14, 15].
The classical models that described drug absorption started long ago with pH-partition theory [16] in which the major factor that was thought to affect the absorption process was the pH-pKa relationship and degree of ionization. This theory took into consideration that the mechanism of absorption is "passive diffusion" and follows "Fick´s laws of diffusion" [17]. However, deviations from this theory were explained according to differences in the unstirred layer, microclimate, and mucous effect [18].
The further step was taken when the lipophilicity and partition coefficient was taken into consideration in the calculation of the absorption potential (AP) of a drug [19, 20].
Several other models were used to get closer models to fit data of drug absorption like the "convective dispersion model" [21], "compartmental model" [22], "microscopic approach" [23]. All these models assume a "homogenous system" that is no longer convincing in light of clear heterogeneity of the gastrointestinal tract (GIT). For example, the upper GIT movement is highly affected by the food state while the movement of the lower part is generally affected by residence and pressure generated by contractions [24]. Studies of Nitmann and VanDamme suggested that movement of chime to more narrow spaces made "friction" and topological distribution of particles more important than diffusion laws [25]. When the less viscous fluid moves toward more viscous fluid, the interface ripples and becomes extremely mending (fractal). Such results were obtained by Bhaskar et al. in studying HCl and pepsin secretion in the stomach [26].
Drug absorption has been described in a homogenous system by equation (1):
qat=Fa.q0.Ka.e-kat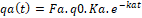 (1)
(1)
Where (qa) is the amount of drug absorbed at the time (t), (Fa) is fraction absorbed, (q0) is the amount of drug, (ka) is first-order absorption rate constant. This model does not comply with stochastic principals [27]. Here, the absorption rate constant is calculated, and the fraction absorbed move exponentially with time as the first-order process. For transporter-mediated absorption, the Michaelis-Menten model was adapted by many scientists [28,29]. The more realistic model should take into consideration the heterogeneity of GIT and fractal principals of drug dispersion described above. The random walk of a diffusing molecule is given by equation (2) [6, 30].
Zt2∝t2/dw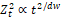 (2)
(2)
Where Zt2 is the mean square displacement of the walker, dw is the random walk dimension (the value of dw is larger than 2, typically 2.8 for 2-dimension and 3.5 for 3-dimension, so the overall exponent is less than 1).
In a homogenous well-stirred system, the rate constant does not change with time. But in heterogeneous systems, this constant is "time dependant" all the time as shown in equation (3) [31].
K=Ko.tλ (3)
(3)
Where K is the time-dependent coefficient, Ko is the constant, and λ is different from zero and it is the outcome of two phenomena, heterogeneity (a geometric disorder of the medium) and the imperfect mixing conditions.
So, for most drugs, the in-vivo dissolution rate constant and absorption rate constant is time-dependent. (Ka =K1tα) if the process is absorption and (Kd=K2tβ) if the process is dissolution.
Thus, the absorption process under these conditions can be described by equation (4) :
qat=Kaqat=K1tα qa(t)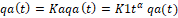 (4)
(4)
Where qa is the dissolved quantity of the drug in the GIT, (α and β ≠0)
Consequently, this equation provides a theoretical basis for the empirical power functions of time-dependent processes [32,33]. The values of ɑ and β link the physic-chemical properties of a drug to the topology of GIT content and the distribution of particles. The late one is very important in fractal kinetics [34].
Based on the above consideration, drugs may be classified broadly to "drugs with homogenous absorption" and "drug with heterogeneous absorption". Drugs with homogenous absorption are those drugs that have enough solubility and permeability which dissolve and absorbed in conditions resemble "well-stirred system" while drugs with heterogeneous absorption kinetics transverse the GIT and exhibit limited bioavailability and high variability [35].
Understanding the fractal nature of the absorption process makes it unreliable to use "mean" or "median" values along with the whole GIT due to the complexity of the process and periods of stasis [36]. Also, poor in-vitro-in vivo correlation is expected for drugs of class II and IV BCS which makes routine dissolution test results not representative of bioavailability and bioequivalence studies [37]. As a result, values of Cmax and AUC measured from large numbers and compared statistically sometimes up to 90%CI and attributed to the "variation" and dispersion error. While in fractal kinetics of absorption, Cmax, Tmax, and AUC are largely dependent on ɑ and β [38]. What is described as "randomness" can be caused by the "time dependency" of the rate coefficient of the in-vivo process [39]?
From the observation above, the comparison of bioavailability parameters in bioequivalency studies may be taken into consideration to a level of outcomes rather than rigorous statistical tests of mean values.
Fractal aspects in drug disposition / Heterogeneity and heterogeneous processes
The routine collection of experimental data in PK is usually done by entering the drug molecules into the system and subsequent sampling at different time intervals to follow the decline of the drug in the plasma due to distribution and elimination processes, then treating data by mathematically by models known as empirical models.
Empirical models include “exponential profile” which differentiates concentration concerning time in which the relative variation of concentration divided by variation of time is constant. In the power-law profile, also the concentration is differentiated vs. time but, the constant represents “relative variation” of concentration divided by “relative variation” of time [40, 41]. While the Gamma profile may be considered a mixture of exponential and power-law [42].
The sum of the negative exponential of data of the previous laws is assumed in the well-stirred compartments. Again, the heterogeneous characteristics of processes in the body like distribution and elimination require the development of more realistic models. Fractal kinetics could be applied to describe kinetic processes under heterogeneous conditions.
Particularly in PK, Macheras, and Savageau were among the first who published on fractal kinetics and modeling [43]. Macheras’s work contributed in the illustrations of fractal aspects in absorption [44], distribution [30,45] stochastic processes [46], Michaelis–Menten metabolism [47], and carrier-mediated transport [48].
Distribution Process
Blood flow in the arteries and veins is subjected to many descriptive models. It is now known that “bifurcating” networks are the characteristics of the vascular network in humans. The blood vessels continuously bifurcate to generate and more branching for approximately 96000 km length of vessels [9].
Van Beak et al. developed a model that describes blood flow in the vascular system. However, the model gives only a simple description of the fractal network but can be used to describe other systems of heterogeneous distribution [49,50].
Regarding drug distribution and movement between the arterioles and venous network, when the drug reaches the area of the arterial-venous junction will enter another heterogeneous environment. Based on this, drug distribution can be classified into two broad classes ; homogeneous distribution and heterogeneous distribution.
Drugs with homogeneous distribution are those drugs with physico-chemical properties that allow them to leave from arteries to the adjacent tissues and reach only well-perfused tissues and return rapidly to veins [51]. These drugs obey homogeneous models of disposition. Thus, the upper part of the vascular system and the well-perfused adjacent system comprise a homogeneous compartment. While, blood flow to the terminal arterioles endings go deep in the tissue and slows down, here the deviation occurs from homogeneous to heterogeneous “unstirred” system. This transport limitation was formally described as “membrane permeability limited transport” in the physiological system [52].
So, in drug distribution that is described inhomogeneous system, a rate constant of drug movement to the tissues is calculated and the process is described as a first-order process [52].
It was found that distribution in disordered media, the value of rate constant is related to the geometry of the media [3]. Here, the diffusion is hindered by geometric heterogeneity which can be expressed in terms of fractal and spectral dimensions. This distribution of drugs can be described using fractal geometry using spectral dimension (ds). For ds ≤ 2, drugs are likely to stay in its original vicinity and re-cross its starting point creating a mesoscopic depletion zone around trap (eg. Enzyme). This dense fluctuation of drug movement results in entailing the macroscopical rate coefficient. Subsequently, the macroscopic reaction rate which is given by deriving n(t) can be described as “efficiency” of diffusing reacting drug as shown in equation (5) [6].
K(t) α n(t) αt –(1-ds/2) = t-λ (5)
Where 0 ≤ λ ≤1 and 0≤ ds≤ 2 and the minus sign refer to the decrease in (k) with time. This time-dependent rate constant in the form of the power law is the expression of microscopic anomalous diffusion in a fractal dimension which leads to anomalous kinetics [53].
Fig (1) shows the difference between homogeneous and heterogeneous distribution in the vascular network [11].
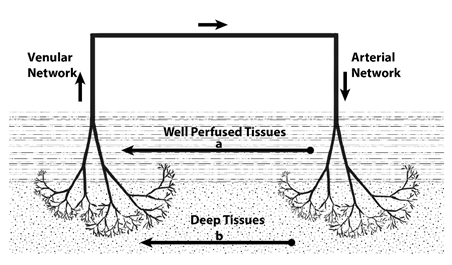
Fig. 1 : Homogeneous (in the well-perfused tissues” versus heterogeneous (in the deep tissues) distribution.
Elimination
Regarding the elimination process in the liver, metabolism, or biotransformation of drugs, the liver has an unusual microcirculatory pathway. The portal vein, hepatic artery, and hepatic vein comprise the microcirculation of the liver. While microcirculation involves hepatic arterioles and sinusoids [54]. The sinusoids form a 3-dimensional network and form interacting channels with the lobules [55].
It has been a long time since the Michaelis-Menten model was established to measure metabolic activity using isolated enzymes or rat liver microsomes :

Where E is an enzyme, S substrate, P product (of metabolism), and ES is enzyme-substrate complex. And the velocity of the reaction was described by the Michaelis-Menten equation.
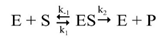 (6)
(6)
Where V is the velocity of reaction, Vmax is the maximum velocity at steady –state, Km is Michaelis-Menten constant (described in equation 7) and S is the substrate in reaction [56].
Km = (K-1+K2)/K3 (7)
Later, to incorporate physical factors and intrinsic clearance of the liver, another equation was developed to describe hepatic clearance under steady-state conditions [57].
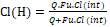 (8)
(8)
Where Cl(H) is hepatic clearance, Q is hepatic blood flow, Fu is fraction unbound of the drug in plasma, and Clint is the hepatic intrinsic clearance.
The establishment of in-vitro-in – vivo correlation is always the major issue of dealing with drug metabolism.
Assuming the “parallel model” that the liver receives blood in parallel series representing the sinusoids, another equation was developed.
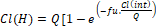 (9)
(9)
In which the relation between ClH and fu. Clint and Q are exponential [58]. However, in both models, again the perfect “mixing” is assumed and there is still difficulty in predicting the in vivo metabolic rate of various drugs.
The fractal aspects in hepatic metabolism are characterized by observing different anatomical characteristics of the liver as it is considered as “fractal object” by many authors because of self-similar structure [59,60]. Javanard examined and measured the fractal dimensions of the liver by using ultra-sounding scattering as df = 2 over a wavelength of 0.15- 1.5mm [61]. So, instead of considering the liver as an organ that is divided into lobules in which blood flow parallel, it is now described according to the fractal design as enzymes adhere along the inner wall in many layers. By this, a large number of enzymes explains the high reaction rate despite time-dependent fractal kinetics [62]. Berry studied the enzymatic reaction using Monte Carlo simulation in a 2-dimensional lattice found that the fractal kinetics are increasingly pronounced as obstacle density, also, the rate constant was a time-dependent coefficient since segregation occurs due to the fractal reaction of the reaction media [63].
Using a flow-limited physiological model, Frite et al. were able to explain the non-linear PK of mibefradil in dogs. They measured the df of the dog’s liver as 1.78-1.91 which is close to 2. [64].
Marsh and Tuzynski introduced a model based on fractal kinetics with anomalous reaction order as a physiologically based mechanism that generates power-law tails using only one compartment. The model was applied to mibefradil metabolism and interpreted in terms of the anatomy of the liver. They concluded that in the under-stirred heterogeneous spaces, the steady-state fractal kinetics describes the kinetics the best, this is due to the continuous influx of drug molecules and recycling in the circulatory system [47].
Kosmidis et al. further investigated the anomalous kinetics of the liver based on the assumption that the substrate molecules are not constant inside the liver and that they exit from the liver at time t and will return to it sometime later. They also assumed that this time of delay is not constant, but it follows Gaussian distribution with mean T and variance σ2, E, and C remain inside the liver and that only P and S get out and return through the circulatory system.
The model differentiated between time differences after I.V bolus dose and oral administration of drug where it enters the liver via the portal vein after it is absorbed. Thus, the mathematical model for the in vivo MM reaction takes the form :

Where pi is the concentration of species i at time t, RSext(t) in Eq. 11 is the arrival rate of S to the liver from the GIT which depends on the way the drug enters the circulatory system in the liver area and may have the following forms :
- I.V bolus injection: RSext(t) = 0 and the system of equation 12 has to be solved with the initial condition ps(t = 0) = S0 > 0.
- Zero-order input : RSext(t) = k0 for t ≤ Ta and 0 for t > Ta, where k0 is a constant and (Ta) is the duration of input from the GIT. The system of equation 13 has to be solved with the initial condition ps(t = 0) = 0.
- First-order input : RSext(t) = kα × X0 × e−kαt where X0 is a constant quantity (initial concentration of drug in the GIT) and ka is the first-order rate constant. Here, also it has been solved with the initial condition ps (t = 0) = 0.
(- a1ps) in equation 11 represents the rate of exit of the drug molecule, and the whole term after the plus sign represents the number of drug molecules that exit at time u and the other term is the probability that a drug molecule that exits at u will return at the liver at time t. We integrate to account for the contribution from all times 0 < u < t.
So, equation 12 gave the generalized rule for the change in concentration due to hepatic metabolism [65].
This assumption took into consideration the re-entrance of the molecules each time the blood enters the liver. This is a major difference from in –vitro enzyme binding studies.
Application of this model on Monte –Carlo simulation and fitness of data of mibefradil by the same research group [58], lead to the development of the time-dependent Km in MM equation which provides a more realistic approach than the conventional MM formalism knowing that equation 13 Was not derived empirically but it was based on MC simulation. s [66].
This version of the MM equation reveals that the rate of the enzyme reaction depends on ps and t. This time dependency of KM(KM = KM0 × th) and (h) is dimensionless exponent, leads to an increase of this term with time (depending also on the value of the exponent, h). This characteristic constitutes the underlying cause for the successful application equation 13 to mibefradil data.
This particular effort infers that fractal kinetics moved from theory to application in which a more realistic dealing with drug metabolism and elimination applied.
CONCLUSION
The aspect of fractal kinetic has been studied by many researchers starting from mathematics and physiology. These studies gave a much better understanding of the heterogeneity of different processes in the human body. The description of these heterogeneous processes involved the basic processes of biopharmaceutics and pharmacokinetics like drug absorption, distribution, and elimination processes via enzymatic reaction in the liver. These new models are developing and need further work to bring them into an application.
Declaration of conflict
We report no conflict to be declared.
ACKNOWLEDGMENT :
I would like to thank Prof. Panos Macheras from National and Kapodistrian University of Athens for being such a great idol for me in science wishing him long preoperative life.
REFERENCES
- Boeing G. Visual analysis of nonlinear dynamical systems : chaos, fractals, self-similarity and the limits of prediction. Systems. 2016 Dec ;4(4):37.
- Hacker M, Messer WS, Bachmann KA. Pharmacology : principles and practice. Academic Press ; 2009 Jun 19.
- Buchanan M. Mathematics : A fractal life. Nature. 2012 Oct 24;490(7421):476.
- Mandelbrot, BB. The Fractal geometry of nature. New-York : Macmillan, 1983.
- Mandelbrot, BB. Fractals and Chaos. Berlin : Springer, 2004.
- El Boundati Y, Ziat K, Naji A, Saidi M. Generalized fractal-like adsorption kinetic models: Application to adsorption of copper on Argan nut shell. Journal of Molecular Liquids. 2019 Feb 15;276:15-2
- Shargel, L., Wu-Pong, S., Yu, A. Applied Biopharmaceutics and pharmacokinetics. New York: McGraw-Hill Education, Medical. 2015 ; Pp 4, 177-180.
- Spruill W, Wade W, DiPiro JT, Blouin RA, Pruemer JM. Concepts in clinical pharmacokinetics. ASHP; 2014 Apr 11.
- Roerig B, Chen B. Relationships of local inhibitory and excitatory circuits to orientation preference maps in ferret visual cortex. Cerebral cortex. 2002 Feb 1;12(2):187-98.
- Kosmidis K, Argyrakis P, Macheras P. Fractal kinetics in drug release from finite fractal matrices. The Journal of chemical physics. 2003 Sep 22;119(12):6373-7.
- Iliadis A, Macheras P. Modeling in Biopharmaceutics, Pharmacokinetics and Pharmacodynamics. Springer, 2006.
- Ma D, Stoica AD, Wang XL. Power-law scaling and fractal nature of medium-range order in metallic glasses. Nature materials. 2009 Jan;8(1):30-4.
- Edgar G. Measure, Topology, and Fractal Geometry. Springer. 2007 ; p. 7
- Pinnamaneni R, Tanneru P, Vaddavalli N, Tatineni J, Tharani R. In silico Drug interaction studies on HIV Integrase. Journal of Biochemical Technology. 2019;10(3):34.
- Dhyani A, Kumar G. A New Vision To Eye: Novel Ocular Drug Delivery System. Pharmacophores. 2019 Apr 1;10(1):13-20.
- Henderson LJ. Concerning the relationship between the strength of acids and their capacity to preserve neutrality. American Journal of Physiology-Legacy Content. 1908 Mar 2;21(2):173-9.
- Macheras P, Karalis V, Valsami G. Keeping a critical eye on the science and the regulation of oral drug absorption : a review. Journal of Pharmaceutical Sciences. 2013 Sep 1;102(9):3018-36.
- Dressman JB, Amidon GL, Fleisher D. Absorption potential: estimating the fraction absorbed for orally administered compounds. Journal of pharmaceutical sciences. 1985 May;74(5):588-9.
- Yang, Q. Dissolution mechanisms : theoretical and experimental investigations. [Dissertation]. University of Iowa, 2015.
- MP SC, Prasobh GR, Jaghatha T, Aswathy BS, Remya SB. An Overview on Liposomal Drug Delivery System. Int. J. Pharm. Phytopharm. Res. 2019;9(2):61-8.
- Ni P, Ho N, Fox J, Leuenberger H, Higuchi W. Theoretical model studies of intestinal drug absorption V. non-steady state fluid flow and absorption. International Journal of Pharmaceutics. 1980 ;5(1), 1980, 33-47.
- Macheras P, Reppas C, Dressman J. Estimate of volume/flow ratio of gastrointestinal fluid in humans using pharmacokinetic data. Pharmaceutical Research 1990; 7(5), 518-5
- Sinko P, Leesman GD, Amidon G L. Predicting fraction dose absorbed in humans using macroscopic mass balance approach. Pharmacological Research. 1991;8(8): 979-988.
- Davis SS, Hardy JG, and Fara JW. Transit of pharmaceutical dosage form through the small intestine. Gut. 1986;27(8):886-892
- Nitmann J, Daccord G, Stanely H. Fractal growth of viscous fingers: A quantitative characterization of a fluid instability phenomenon. Nature. 1985; 314: 141-144.
- Bhaskar K, Garik P, Turner B, Bradley J, Bansil R, Stanely H, LaMont J. “Viscous fingering of HCl through gastric mucin. Nature. 1992; 360 (6403): 458-461.
- Veng-Pedersen P, Modi N. Optimal extravascular dosing intervals. Journal of Pharmacokinetic and Biopharmaceutics. 1991; 19(4):405-412.
- Riad LE, Chan KH, Ronald WE, Sawchuk J. Simultaneous First- and Zero-Order Absorption of Carbamazepine Tablets in Humans. Journal of Pharmaceutical Sciences. 1986; 75 (9): 897-900
- Hacker M, Messer WS, Bachmann KA. Pharmacology: Principles and Practice, USA, Academic Press. 2009 ; p 80.
- Macheras P. A Fractal Approach to Heterogeneous Drug Distribution: Calcium Pharmacokinetics. Pharmaceutical Research. 1996; 13(5):663–670.
- Pang KS, Weiss M, and Macheras P. Advanced Pharmacokinetic Models Based on Organ Clearance, Circulatory, and Fractal Concepts. The American Association of pharmaceutical sciences journal. 2007; 9(2): 268-283.
- Verotta D. Two constrained deconvolution methods using spline function. Journal Pharmacokinetics and Biopharmaceutics. 1978;21(5): 227-241.
- Veng-Pedersen, P. An algorithm and computer program for deconvolution in linear pharmacokinetics. Journal Pharmacokinetics and Biopharmaceutics. 1980;8(5): 463-48.
- Macheras P, Argyrakis P, and Polymilis C. Fractal geometry, fractal kinetics, and chaos in route to biopharmaceutical sciences. European Journal of Drug Metabolism and Pharmacokinetics.1996;21(2):77-86.
- Macheras P, Argyrakis P. Gastrointestinal drug absorption: is it time to consider heterogeneity as well as homogeneity? Pharma Res. 1997 ; 14(7):842-847.
- Scher H, Shlesinger M, Bendler J. Time scale invariance in transport and relaxation. Physics Today.1991;44(1):26-34.
- Lu Y, Kim S, Park K. In vitro-In vivo Correlation: Perspectives on Model Development. International Journal of Pharmaceutics. 2011;418(1): 142–148.
- Tsang Y, Pop R, Gordon P, Hems J, Spino M. High variability in drug pharmacokinetics complicates determination of bioequivalency of bioequivalent: Experience with verapamil. Pharmaceutical Research. 1996;13(6):846-850.
- Kalampokis A, Argyrakis P, Macheras P. Heterogeneous tube model for the study of small intestinal transit time flow. Pharmaceutical Research. 1999;16(1): 87-91.
- Weiss M. A note on the role of generalized inverse Gaussian distribution of circulatory transit in pharmacokinetics. Journal of Mathematical Biology. 1998; 20: 95-102.
- Uros R, Blardi P, Giorgi G.A short introduction to pharmacokinetics. European Review for Medical and Pharmacological Sciences. 2002;6: 33-44.
- Weiss M. Negative power functions of time in pharmacokinetics and their implications. Journal of Pharmaceutics and Biopharmaceutics. 1985;13 (3): 309-346.
- Macheras P. Carrier-mediated transport can obey fractal kinetics. Pharmaceutical Research. 1995;12(4) :541–548.
- CaroliBosc FX, Iliadis A, Salmon L, Macheras P, Montet A M, Bourgeon A, Garr R, Delmont J P, Montet J C. Ursodeoxycholic acid modulates cyclosporin A oral absorption in liver transplant recipients. Fundamentals of Clinical Pharmacology. 2000;14: 601–609.
- Dokoumetzidis A, Macheras P. 2003.A tube model for transport and dispersion in the circulatory system based on the vascular fractal tree. Annu Rev Biomed Eng. 31:284–293.
- Claret L, Iliadis A, Macheras P. A stochastic model describes the heterogeneous pharmacokinetics of cyclosporine. Journal of Pharmacokinetics and Pharmacodynamics. 2001;28(5): 445–463.
- Marsh R, Tuszynski J A. “Fractal Michaelis–Menten kinetics under steady-state conditions: Application to mibefradil. Pharmaceutical Research. 2006; 23(12) :2760–2767.
- Ogihasra T, Tamai I, Tsuji A. Application of fractal kinetics for carrier-mediated transport of drugs across intestinal epithelial membrane”. Pharmaceutical Research. 1998; 4:620–625.
- Van Beek JHGM, Roger SA, Bassingthwaighte JB. Regional myocardial flow heterogeneity explained with fractal networks. American Journal of Physiology. 1989; 26: 1670–1680
- Rezania V, Marsh R, Coombe D, Tuszynski J. A physiologically-based flow network model for hepatic drug elimination I: regular lattice lobule model. Theoretical Biology and Medical Modeling. 2013;10 (52) PMC3833673.
- Terasaki T, Sugiyama Y, Iga T, Sawada Y, Hanano M. Theoretical consideration of drug distribution kinetics in a noneliminating organ: comparison between a “homogeneous (well-stirred) model and nonhomogeneous (tube) model. Journal of Pharmacokinetics and Biopharmaceutics. 1996; 13(3); 265-287.
- Rescigno AThe rise and fall of compartmenta analysis. Pharmacological Research. 2001; 44: 337–342.
- Farris F, Dedrick R, Allen P, Smith J. Physiological model for the pharmacokinetics of methyl mercury in the growing rat. Toxicology and Applied Pharmacology. 1993; 119(1): 74-90.
- Campra J, Reynolds T. 1982.The hepatic circulation in the liver. Biology and Pathology, edited by Arias, I., Pipper, H., Schacher, D., and Shafritz, D. New York, Raven Press.
- Glenny R and Robertson H. Fractal properties of pulmonary blood flow: characterization of spatial heterogeneity. Journal of Applied Physiology. 1990; 69(2):532-545.
- Michaelis L , Menten ML. Die Kinetik der Invertinwirkung (The Kinetics of Invertase Action). Biochemische Zeitschrift 1913; 49:333–369.
- Johnson KA, Goody RG. The Original Michaelis Constant: Translation of the 1913 Michaelis-Menten Paper. Biochemistry. 2011;50 (39): 8264–8269.
- Lucas A, Sproston J, Barton P Riley R. Estimating human ADME properties, pharmacokinetic parameters, and likely clinical dose in drug discovery. Expert Opinions in Drug Dispositions. 2019;14(12): 1313-1327.
- Norwich K. Noncompartment models of whole-body clearance of tracers: A review. Annuals in Biomedical Engineering. 1997; 25: 421-439.
- Gaudio, E, Chaberek, S, Montella, A, Pannarale, L, Morini, S, Novelli, G, Borghese, F, Conte D, Ostrowski K. Fractal and Fourier analysis of the hepatic sinusoidal network in normal and cirrhotic rat liver. Journal of Anatomy. 2005; 207(2): 107–115
- Javanard, G. The application of a fractal model to the scattering of ultrasound in biological media. The Journal of the Acoustical Society of America.1989; 86(2): 493-496.
- Zhu, Y, Gao, W, Guo, Z, Zhou Y, Zhou Y. Liver tissue classification of in-face images by fractal dimension‐based support vector machine. Journal of Biophotonics. 2020; 60:154-150.
- Berry, H. Monte Carlo simulation of enzymes reaction in two dimensions: Fractal kinetics and spatial segregation. Biophysical Journal. 2002;83(4): 1891-1901.
- Uribe, B, Gonzal, O, Blanco, M, Albóniga, OE, Alonso, ML, Alonso, RM. Analysis of the Heterogeneous Distribution of Amiloride and Propranolol in Dried Blood Spot by UHPLC-FLD and MALDI-IMS. Molecules. 2019; 24(23): 4320-4330.
- Kosmidis, K, Karalis, V, Argyrakis, P, Macheras, P. Michaelis-Menten Kinetics under Spatially Constrained Conditions: Application to Mibefradil Pharmacokinetics. Biophysical Journal. 2004; 87 (3):1498-1506.
- Isvoran, A, Vilaseca, E, Ortega, F, Cascante, M, Mas, F. About implementing a Monte Carlo simulation algorithm for enzymatic reactions in crowded media. Journal of Serbian Chemical Society. 2006;71 (1) 75–86.
